Building Strong Foundations: Recursion in C Explained

Recursion is a fundamental idea in computer programming that allows functions to call themselves, making it an effective tool for solving complex problems by breaking them down into smaller subproblems. Recursion is unique in C programming because of its simplicity and beauty in solving various problems. We will examine the concepts, methods, and uses of recursion in C in-depth in this comprehensive guide.

What is Recursion?

In computer programming, recursion is a concept that a function can call itself within its definition. It resembles a group of Russian dolls nestled inside one another, with a tiny doll inside each larger one.

A function that calls itself to solve a problem is known as recursion in programming. It’s like a mirror that reflects itself infinitely. Instead of solving a problem directly, you break it down into smaller, comparable issues until you reach a base case, which is the most basic version of the problem that does not require any more deconstruction.

Why Use Recursion?

Recursion is very effective when you have a problem that can be divided into smaller, related subproblems. It’s like having a large puzzle to solve piece by piece. Recursion breaks down difficult problems into smaller, more manageable pieces, which helps to simplify them.

Basic concepts in Recursion

Structure of a Recursive Function in C:

A recursive function in C is just like any other function, but with a special ability: it can call itself.
Here’s a simple structure of a recursive function in C:

return_type function_name(parameters) {
    // Base case (condition to stop recursion)
    if (base_condition) {
        return base_value;
    }
    // Recursive case (calling the function itself)
    else {
        // Modify parameters for next recursive call if necessary
        // Recursive call
        return function_name(modified_parameters);
    }
}

Flow Chart Of Recursion in C

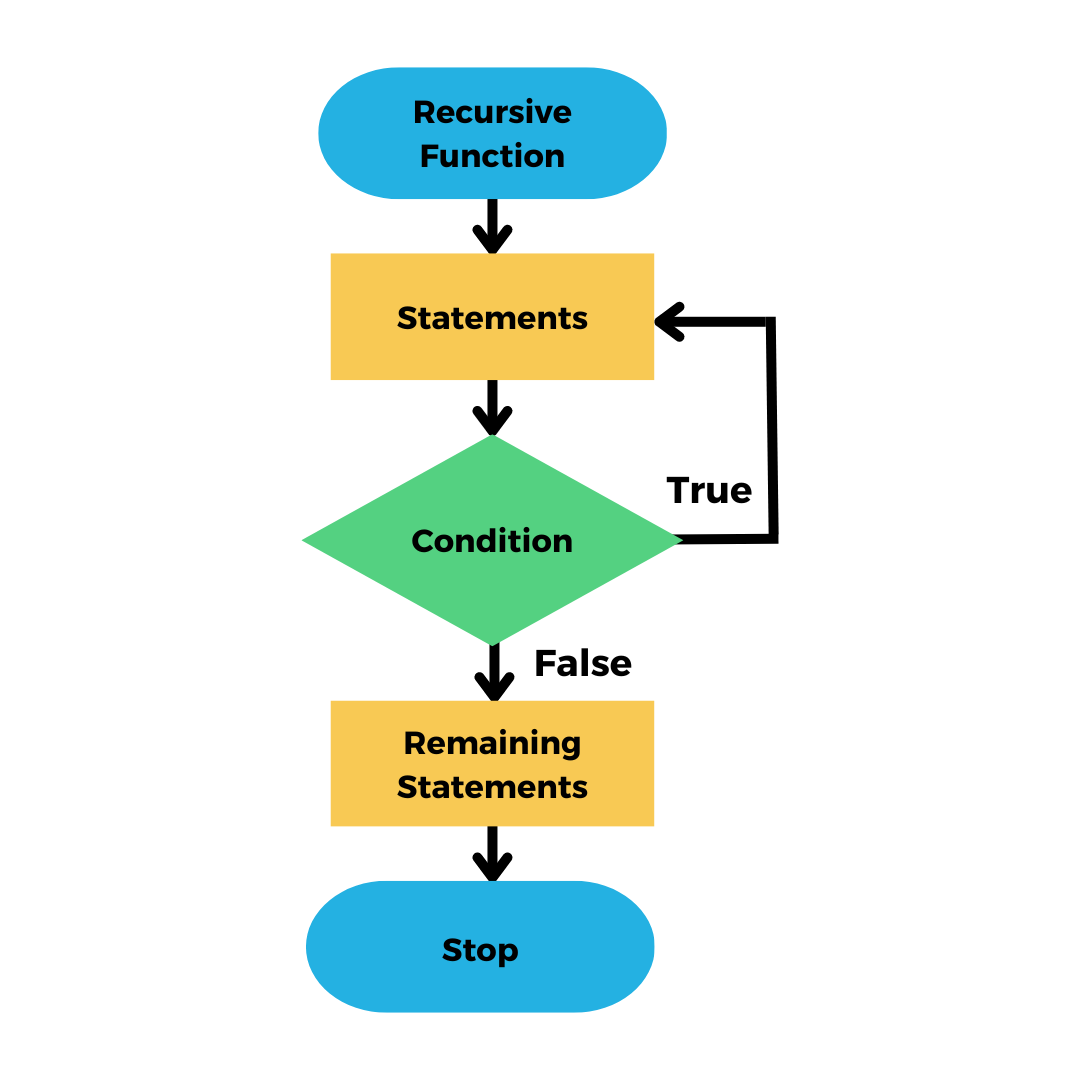
There are two key concepts in recursion: the base case and the recursive case.

Base case: The recursion stops at this point. The condition informs the function when to stop calling itself. Without a base case, the function would call itself endlessly, resulting in a stack overflow error.
Recursive case: This is where the magic happens. In the recursive situation, the function calls itself using a modified version of the original problem. This enables the function to divide the problem into parts until it reaches the base case.

Types of Recursion

1. Linear Recursion:

The most common type is linear recursion, in which a function calls itself exactly once in each recursive situation until it reaches the base case.
Factorial calculation is a well-known example of linear recursion.

int factorial(int n) {
    if (n == 0) {  // Base case
        return 1;
    } else {
        return n * factorial(n - 1);  // Recursive case
    }
}

In this example, the function factorial calls itself recursively with n - 1 until n becomes 0, which is the base case.

2. Tail Recursion:

Tail recursion occurs when the recursive call is the function’s final operation before returning its value.
Example: calculating the sum of elements in an array.

int sum(int arr[], int n, int total) {
    if (n == 0) {  // Base case
        return total;
    } else {
        return sum(arr, n - 1, total + arr[n - 1]);  // Recursive case
    }
}

In this example, the recursive call sum(arr, n - 1, total + arr[n - 1]) is the last operation performed before returning.

3. Binary Recursion:

Binary recursion requires two recursive calls in each recursive case.
Example: calculating Fibonacci numbers.

int fibonacci(int n) {
    if (n <= 1) {  // Base case
        return n;
    } else {
        return fibonacci(n - 1) + fibonacci(n - 2);  // Recursive case
    }
}

In this example, the function calls itself twice (fibonacci(n - 1) and fibonacci(n - 2)).

4. Mutual Recursion

When two or more functions are defined in terms of one another, mutual recursion takes place.
Example: Using mutual recursion to determine if a number is even or odd.

int is_even(int n);

int is_odd(int n) {
    if (n == 0) {
        return 0;  // Even
    } else {
        return is_even(n - 1);
    }
}

int is_even(int n) {
    if (n == 0) {
        return 1;  // Odd
    } else {
        return is_odd(n - 1);
    }
}

In this example, is_even and is_odd call each other to determine if a number is even or odd.

5. Nested Recursion

When a recursive function calls itself again using its own result as an argument, this is known as nested recursion.
For example, compute the Ackermann function.

int ackermann(int m, int n) {
    if (m == 0) {
        return n + 1;
    } else if (n == 0) {
        return ackermann(m - 1, 1);
    } else {
        return ackermann(m - 1, ackermann(m, n - 1));
    }
}

In this example, ackermann calls itself with the result of another invocation of ackermann.

Advantages and Disadvantages of Recursion in C

Advantages of Recursion in C:

Simplifies code structure by dividing complex problems into smaller, more manageable tasks.
Mirroring the problem-solving process improves algorithm readability and understanding.
Allows for a more simple implementation of some algorithms, such as tree traversal or backtracking.
Allows for elegant and concise solutions to naturally recursive conditions.
Can result in more efficient solutions to specific issues than iterative approaches.

Disadvantages of Recursion in C:

May cause performance concerns due to function call overhead and stack utilisation, particularly for highly nested or poorly optimised recursive functions.
When dealing with enormous input quantities or infinite recursion, it is prone to stack overflow faults if not properly implemented.
In order to prevent infinite loops, it is necessary to carefully evaluate base cases and termination conditions.
Some programmers may find it more difficult to debug and understand compared to iterative solutions.
Not suitable for all problems, especially those requiring iterative or non-recursive techniques for maximum efficiency.

Recursion vs. Iteration

Aspect	Recursion	Iteration
Definition	A process where a function calls itself directly or indirectly until a base case is reached.	A process of repeatedly executing a set of instructions until a specific condition is met.
Mechanism	Function calls itself to break down the problem into smaller subproblems.	Uses loops (e.g., for, while) to repeatedly execute a block of code.
Base Case	Requires a base case to terminate the recursive calls.	Requires a condition to be met to exit the loop.
Control Flow	Control flow can be harder to follow due to recursive calls.	Control flow is typically more straightforward and linear.
Memory Usage	Recursive calls utilize call stack memory, potentially leading to stack overflow for large inputs.	Typically uses less memory compared to recursion as it doesn’t involve additional function calls.
Code Complexity	Can lead to simpler and more elegant code for certain problems.	Sometimes requires more lines of code, but can be more intuitive for certain tasks.
Examples	Factorial calculation, Fibonacci sequence generation.	Looping through arrays, searching algorithms (e.g., linear search, binary search).

Table of Contents